HOG 개괄정보는 이전 포스팅을 참고해주세요!
[정리]Histograms of Oriented Gradients for Human Detection (HOG) -1
Histograms of Oriented Gradients for Human Detection [feature extraction을 위한 feature descriptor:HOG descriptor] -Navneet Dalal and Bill Triggs Abstract 논문은 테스트 케이스로 선형 SVM을 기반으로..
studyingfox.tistory.com
Gradient Computation
HOG descriptor를 계산하려면, 수평 & 수직 변화량(그레디언트)를 계산해야 한다.
즉, x 방향으로 픽셀 값 차이를 구하고 y 방향도 동일하게 계산한다는 뜻이다.
논문에서는 uncentred [-1,1], centred[-1,0,1], cubic corrected [1, -8, 0, 8 -1], 3*3 sobel , 2*2 diagonal 커널(?)마스크(?)등으로 테스트 해봤다고 하지만 간단한 [-1, 0, 1] 커널이 가장 좋은 결과를 냈다고 한다.
그레디언트를 계산해보자!-1
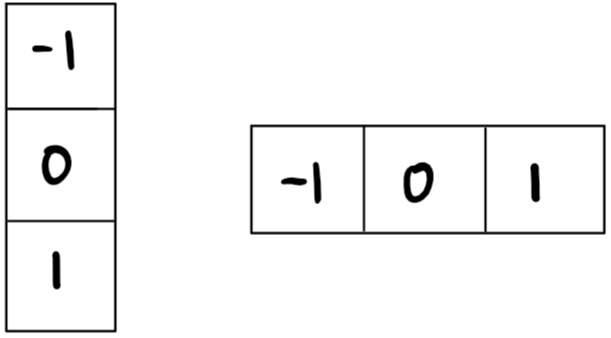
그림 1에서 숫자가 있는 칸은 픽셀이고, 위에서 언급한 [-1,0,1]을 x 방향 계산과 y방향 계산에 맞게 구성하였다.

이제 그림 1에 그림 2를 적용해 각 방향 별 변화량(그레디언트)를 계산해보기 전에!
그림 2에 적용할 커널이 1*3, 3*1이기 때문에 85를 기준으로 68, 78, 89, 56만 필요한 셀이 된다.
먼저 y방향 계산을 해보자.
그림 2에 나온 픽셀을 보면 중앙에 빨간색에 값이 85인 픽셀이 있다. 이 픽셀을 기준으로 y방향 커널을 적용해보면
= 68*(-1) + 85*0 + 56*1 = -68 + 56 =-14 가 나온다.
x방향으로 계산하게 되면
= 78*(-1) + 85*0 + 89*1 = -78 + 89 = 11 이 나온다.
이런식으로 계산하면 그림 2는 다음과 같이 셋팅된다.

그래서 이미지에 있는 모든 픽셀에 지금까지 한 계산이 적용된다.
그레디언트 계산 마지막 단계는 기울기를 이용해 크기(magnitude)와 방향(direction 또는 orientation)을 결정하는 것이다.
그레디언트를 계산해보자!-2
크기와 방향을 구하기 위해선 중학교에서 배운 피타고라스 정리를 먼저 기억 저편에서 가져와야 한다.

앞서 그레디언트가 x,y축의 변화량(기울기)이라 했다. 그렇다면 그레디언트의 크기는 변화량의 크기와 같다는 것!
따라서, 그레디언트의 크기는 아래 수식이 되고,
수식에 이전에 구한
와
의 값을 계산해 그레디언트 크기를 구하면 소수 둘째자리에서 반올림해 17.8이 나온다.
하지만 논문에 따르면 루트 없이 계산한 크기가 더 성능이 좋다고 한다.
방향을 구하기 위해선 각 tan(탄젠트)의 역삼각함수인 arctan(아크탄젠트)를 사용했다고 한다.
먼저 Φ를 구하기 위해 tan(Φ)부터 구한다.
그리고 Φ를 구하기 위해 역삼각함수인 arctan의 값을 구한다.
위에서 구한 와
를 계산해 소수점 둘째자리에서 반올림하면 -51.8이 나온다.
(인터넷에서 공학용 계산기 돌려봤는데 정확하게 한건지 잘 모르겠다.. 피드백 부탁드립니다!)
Spatial/Orientatioin Binning
논문에서 이 부분에 해당하는 곳을 읽다보면 "vote", "weighted vote"등의 단어가 나온다.
이 논문을 읽을 당시 한참 선거철이라 vote를 보면 어떤 사람을 뽑아야 하는지만 떠올랐...기에 이번에 이해를 해보았다.
Vote는 투표한다는 뜻이다. 그래서 말 그대로 투표를 한다(밀어준다가 조금 더 맞을 것 같기도하고..?)
지금부터 천천히 투표한다는 뜻을 알아봅시다요.
히스토그램은 연속 데이터 셋에서 구간별 빈도수를 나타낸 그래프이다. X축은 구간을, Y축은 빈도수를 뜻한다.
그래서 앞에서 계산한 방향(orientation)구간(bin)을 X축에, 빈도수를 Y축에 나타낼 것이다.
논문에 따르면 bin이 9개일때 성능이 많이 향상되며 0~180도에 공간에 있을때 해당된다고 한다.
우선 그레디언트 방향(orientation)을 9개 bin으로 quantization한다.
앞서 9개 bin+0~180도라고 밝혔기 때문에 bin 하나에 20도로 계산하면 된다.
즉 이 단계는 이미지를 8*8 셀로 나누고 이에 대한 그레디언트 히스토그램을 계산하는데,
이 과정에 vote라는 특성(?)을 이용하겠다는 것이다.
Dividing Image

그림 5는 한 이미지에 패치를 나눈 것이다.
8*8로 이미지를 나눈 이유는 더 간단한 representation이 제공되고, 패치로 히스토그램을 계산하면 노이즈에 덜 민감하기 때문이다.
그리고 8*8 사이즈는 원하는 feature를 찾기에 충분히 크기에 해당 크기로 진행되었다.
Gradient of Cell

그림 6에서 중앙에 있는 사진은 패치 하나를 확대해 8*8로 셀을 나누고 화살표로 그레디언트 방향과 크기를 보여주는 것, 오른쪽에 있는 숫자들은 8*8셀의 그레디언트 크기과 방향을 나타내는 숫자이다. 참고로 오른쪽에 있는 Gradient Magnitude와 Direction의 숫자는 가운데 있는 화살표 8*8 셀와 대응되는 값이다.
그레디언트를 나타내는 숫자는 0~180 사이로 구성되어 있고, 양수일 때 실험 결과가 더 잘 나왔기 때문에 음수는 범위는 사용하지 않는다.
그리고 그림 6을 기반으로 히스토그램을 만들 수 있다.
Voting & Making histogram

그림 7을 보면 파란색과 빨간색으로 원과 선이 있다.
먼저, 파란색부터 계산해보자.
Direction(Orientation)에 있는 픽셀은 80, Magnitude는 2 일때, 히스토그램에서 구간이 80인 곳에 2를 쓴다.
빨간색도 동일하게 적용해보면
Direction(Orientation)에 있는 픽셀은 10, Magnitude는 4 일때, 히스토그램에서 구간이 10인 곳에 2를 쓴다. 하지만! 이 문제에서 구간은 20단위로 잘랐기 때문에 2를 쓸 수 있는 공간이 없다.
따라서 10은 0과 20의 반절이기 때문에 구간이 '0'인 곳과 '20'인 곳에 Magnitude를 반으로 나눠 각각 2씩 쓸 수 있다.
여기서 한 가지 추가하자면, 이렇게 구간에 해당값을 추가하는 것을 vote 이라고 한다.
그런데 문제가 있다. 만약 Direction 값이 160을 넘어간다면 어디에 Magnitude 값을 넣어야 할까?
=>Magnitude에 가중치를 부여하자!

그림 8에서 Direction 값은 165, Magnitude 값은 85이다.
이 경우, 가중치를 구해 Magnitude에 곱하여 0과 160 구간에 값을 넣을 수 있다.
가중치를 구하는 방법은
0 구간의 경우, 가 되고, 160 구간의 경우
가 된다.
여기서 분모는 bin의 범위를 뜻한다.
따라서 0 구간에는 21.25가, 160구간에는 63.75가 들어간다.

지금까지 계산한 방식으로 vote를 하며 히스토그램 값을 채우면 그림 9와 같은 히스토그램을 만들 수 있다.
결국 나흘 넘게 애써서 gradient computation이랑 spatial/orientation binning을 다 포스팅하는 기적이 일어났다...후
한 문단 이해하는데 너무 오래 걸려서 포스팅 하기 힘들었지만 뿌듯함...이 남았다 크크
과연 다음 포스팅은 마무리를 지을 수 있을지~!~!~!~!???????
참고
http://imloil.blogspot.com/2016/12/opencv-hog-with-paper-2-compute.html
https://www.learnopencv.com/histogram-of-oriented-gradients/



